One of the main theories in motor control is that in order to move accurately, the brain forms internal models that learn to predict the sensory consequences of motor commands. Evidence for this idea comes from human behavioral experiments and animal lesion studies, suggesting that a critical structure for forming internal models is the cerebellum. However, it has been difficult to decipher how, at the neuronal level, the cerebellum represents internal models: while for some tasks like smooth pursuit eye movements the activity of cerebellar Purkinje cells (P-cells) appears to predict velocity of the eye, for most other movements such as saccadic eye movements, wrist movements, or arm movements, it has been difficult to relate activity of P-cells to the actual motion. That is, if the P-cells are encoding an internal model, that encoding is not obvious.

Because learning likely involves a change in the neural encoding, the poor understanding of the neural encoding of internal models has made it difficult to decipher how experience of an error changes the encoding, and how that change in the encoding improves control of movements. The problem, therefore, is fundamentally about understanding neural encoding in the cerebellum.

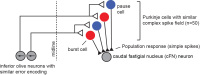
Recently, our team described a new idea. We imagined that the P-cells of the cerebellum are organized in micro-clusters, where each micro-cluster is composed of P-cells that project onto a single output neuron (in the deep cerebellar nucleus). Importantly, the P-cells that form a micro-cluster share a specific property: a common preference for error. The preference for error in an individual P-cell is expressed through its complex spike activity. Therefore, one way to test our idea was through organizing the simple spikes of the P-cells based on functional properties of each P-cell’s complex spikes.

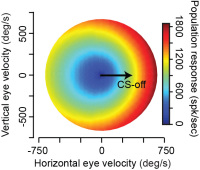
A large body of P-cell data from the cerebellum had been collected by our colleagues Dr. Robi Soetedjo and Dr. Yoshiko Kojima at Univ. of Washington. We analyzed that data using the micro-cluster hypothesis and found something interesting: the population response of the simple spikes of the P-cells precisely predicted motion of the eyes during a saccade via a gain-field. That is, if the P-cells were organized into groups wherein we measured the simple spikes generated by only the cells that shared the same preference for error, then the population response exquisitely predicted motion of the eyes as a multiplicative interaction between real-time speed and direction of motion. Because a gain-field encoding had earlier been found for representation of eye movements in the posterior parietal cortex, and for representation of arm movements in the motor cortex, our observations in the cerebellum raised the possibility that there was a common principle of encoding in disparate regions of the motor system.

​There are a couple of good puzzles regarding the question of how the brain controls behavior. The first puzzle is with regard to how the brain makes a decision. The second puzzle is with regard to how it performs actions. For example, at the breakfast table, you consider the various options and choose to reach for the bagel. The way you deliberated various options, and arrived at your choice, is the decision-making part. The way you reached is the motor-control part.

The first puzzle is studied in the field of decision-making using a framework in which a utility is assigned to each potential action. This utility depends on the reward at stake, and the effort that may be required to perform that action. The action that is chosen is often the one that has the highest utility. The second puzzle is studied in the field of movement-control using a framework in which a cost is assigned to each potential sequence of motor commands. The motor commands that are chosen, i.e., the speed of the movement and its trajectory, are the ones that minimize this cost. In a sense, the field of decision-making has been concerned with the question of what to do, whereas the field of motor-control has been concerned with the question of how to perform the selected movement.

We think, however, that the two puzzles are related. Both the decision of which movement to perform, and the ensuing movement, is influenced by the purpose of the movement: a movement that is associated with a high utility is not only preferred, but it is also performed with greater vigor (faster).  For example, animals not only prefer a stimulus that promises greater reward, but also move faster toward that stimulus. You walk faster toward someone you love, as compared to someone you don't like as much. These observations suggest that while the utility of an action depends on the reward at stake and the required effort (dictating which stimulus to move toward), the same variables also influence how the brain performs the action (dictating vigor of the ensuing movement). We have been working on formulating a unified framework in which we can understand both the decision that the brain makes as to which action to perform, and the details of the movement that follows that decision.

In collaboration with Prof. Alaa Ahmed at University of Colorado, we recently proposed a mathematical framework that attempts to unify motor-control with decision-making. The basic idea is that the way we make decisions, and the way we move, are related because both aim to maximize a common utility, and because in our brain, many of the neural circuits that care about reward and effort in decision-making, are shared with the circuits that control movements. And so perhaps the trait-like features of our individuality is reflected in not only the way we make decisions, but also the way we move. As a result, when disease affects one aspect of our behavior (decision-making), it can also affect the other (motor-control).

For example, some of the neural circuits  that are involved in representing reward and effort are located in the basal ganglia, and these circuits are damaged in Parkinson's disease. Perhaps this produces consistent deficits in both decision-making and motor control. We recently showed that through non-invasive brain stimulation, some of the symptoms associated with perception of effort could be allieviated in some PD patients. Our current research is investigating the relationship between decision-making and movement vigor in healthy people, as well as in people who suffer from Parkinson's disease. 

All movements end in a period of stillness. However, stillness is not inactivity. Rather, during stillness muscles receive sustained, balanced inputs that actively maintain limb position. For example, to reach a target, the brain engages the various muscles in a coordinated fashion, and then when the reach ends, the muscles are engaged with sustained commands that hold the limb at the target. What is the neural basis of the system that generates these hold commands?

Current models assume that reaching and holding are controlled in sequence: one system moves the arm, and then once the movement is over, another system holds it still. A feature of these models is that the hold period commands depend only on the target location, not the commands that brought the arm to that location. Moreover, it is thought that the motor cortex is responsible for generating the “dynamic” commands that move the arm, as well as the “static” commands that subsequently hold it. Our results, however, challenges both assumptions. The data suggest that the hold period commands depend not just on the target, but also the commands that brought the limb to the target. Furthermore, the data hint that an unknown, possibly subcortical system may be privy to the ongoing move commands generated by the cortex, integrating them to influence the commands that hold the limb.

These new data are intriguing because on the one hand, they suggest a new computational model for control of reaching. More importantly, the data are interesting because they potentially shed new light on the relationship between movement and postural deficits in stroke survivors: it is possible that in hemiparesis, the movement and postural deficits are not independent symptoms, but related.

In our experiments, we focused on active holding following reaching and found that in the paretic arm, the sustained commands during the hold period were abnormal, but that abnormality had structure. The hold commands appeared to be a result of normal integration of the preceding commands that moved the arm to its current location. One model (but certainly not the only one) is that following damage to the corticospinal tract, some of the abnormal commands generated during the hold period may be due to normal subcortical integration of the poor commands generated by the cortex during the previous reach period.